การของ อาร์คีมีดีส มาใช้ จนในที่สุดเขานำมาประดิษฐ์เป็นเครื่องจักรไฮดรอลิกที่มีประโยชน์อย่างมากในการยกน้ำหนักและยังได้ อธิบายหลักการของความดันของเหลว พ่อของปาสคาลทำหน้าที่เป็นหน่วยเก็บภาษีให้รัฐบาลฝรั่งเศสครอบครัวของเขาจึงต้องยุ่งเกี่ยวกับเรื่องตัวเลขของเงิน ทองจำนวนมากด้วยความติดที่อยากจะหาเครื่องจักรเข้ามาช่วยเป็นเครื่องคำนวณคิดเลขเขาได้ประดิษฐ์เครื่องคิดเลขแบบ กลไกขึ้น เขาใช้เวลาถึง 3 ปีในการประดิษฐ์ และสร้างขึ้นมาใช้งาน และประสบผลสำเร็จด้วยดี ปาสคาลแสดงให้เห็นความเป็นคนช่างคิด และพัฒนาอย่างดียิ่งเพียงเมื่อเขามีอายุได้ 16 ปีปาสคาลได้เสนอผลงงานวิจัย ในบทความที่เขานำเสนอ ได้แก่ "Essay on Conic Sections" ซึ่งเป็นเรื่องราวเกี่ยวกับรูปตัดกรวยที่แสดงการวิเคราะห์เชิงเรขาคณิตและคณิตศาสตร์ที่เกี่ยวข้อง ต่อมาปาสคาลได้มีโอกาสศึกษาวิชาคณิตศาสตร์ชั้นสูงขึ้นกับแฟร์มาตโดยเฉพาะ อย่างยิ่งเรื่องรากฐานแคลคูลัส และทฤษฎีความน่าจะเป็น  เขาทำความเข้าใจหลักและทฤษฎีหลายอย่างของยูคลิดได้ก่อนอายุ 12 ปี นอกจากนี้เขามีความสนใจในเรื่องวิชาฟิสิกส์โดยเฉพาะในเรื่องของเหลวและแรงดันของเหลวโดยนำหลักการของ อาร์คีมีดีส มาใช้ จนในที่สุดเขานำมาประดิษฐ์เป็นเครื่องจักรไฮดรอลิกที่มีประโยชน์อย่างมากในการยกน้ำหนักและยังได้ อธิบายหลักการของความดันของเหลว
พ่อของปาสคาลทำหน้าที่เป็นหน่วยเก็บภาษีให้รัฐบาลฝรั่งเศสครอบครัวของเขาจึงต้องยุ่งเกี่ยวกับเรื่องตัวเลขของเงิน ทองจำนวนมากด้วยความติดที่อยากจะหาเครื่องจักรเข้ามาช่วยเป็นเครื่องคำนวณคิดเลขเขาได้ประดิษฐ์เครื่องคิดเลขแบบ กลไกขึ้น เขาใช้เวลาถึง 3 ปีในการประดิษฐ์ และสร้างขึ้นมาใช้งาน และประสบผลสำเร็จด้วยดี
ปาสคาลแสดงให้เห็นความเป็นคนช่างคิด และพัฒนาอย่างดียิ่งเพียงเมื่อเขามีอายุได้ 16 ปีปาสคาลได้เสนอผลงงานวิจัย ในบทความที่เขานำเสนอ ได้แก่ "Essay on Conic Sections" ซึ่งเป็นเรื่องราวเกี่ยวกับรูปตัดกรวยที่แสดงการวิเคราะห์เชิงเรขาคณิตและคณิตศาสตร์ที่เกี่ยวข้อง ต่อมาปาสคาลได้มีโอกาสศึกษาวิชาคณิตศาสตร์ชั้นสูงขึ้นกับแฟร์มาตโดยเฉพาะ อย่างยิ่งเรื่องรากฐานแคลคูลัส และทฤษฎีความน่าจะเป็น ผลงานอย่างหนึ่งที่เรารู้จักกันดีคือ สามเหลี่ยมปาสคาล ซึ่งเป็นตัวเลขที่จัดทรงเป็นรูปสามเหลี่ยม ซึ่งในชีวิตประจำวันของเราเกี่ยวข้องกับตัวเลขเหล่านี้อยู่มาก
สามเหลี่ยมปาสคาล
ความมหัศจรรย์ของสามเหลี่ยมปาสคาล
ผู้ค้นพบสามเหลี่ยมปาสคาล
ชุดของจำนวนทีในปัจจุบันเราเรียกว่า “สามเหลี่ยมปาสกาล” ได้รับการความสนใจในการศึกษาจากคณิตศาสตร์ทั้งในอินเดีย กรีก จีน ก่อนหน้านั้นนานแล้ว แต่ทว่า แบลส ปาสกาล (ค.ศ. 1623 – 1662) เป็นบุคคลแรกที่ค้นพบและแสดงให้เห็นความสำคัญ และแบบรูปทั้งหมดที่บรรจุอยู่ในสามเหลี่ยมปาสกาล นี่เองเป็นสาเหตุที่ทำให้เราเรียกมันว่า “สามเหลี่ยมปาสกาล” เพื่อให้เกียรติแก่ปาสกาลซึ่งเป็นค้นพบแบบรูปของมัน
แต่เราก็ยังพบว่าในบางตำรา เรียกมันว่า “สามเหลี่ยมของชาวจีน” (Chinese’s Triangle) ด้วย เพื่อให้เกียรติแก่ชาวจีนโบราณที่ได้ค้นพบ และพัฒนาขึ้นในระยะแรก ชนชาติใดบ้างที่สนใจศึกษาเรื่องนี้
ชนชาติที่ให้การศึกษาเรื่องนี้ก่อนที่ปาสกาลจะค้นพบความสวยงามทั้งหมดของสามเหลี่ยมนี้ในงานของเขาที่ชื่อ Traité du triangle arithmétique (1653) เริ่มเดิมทีเป็นแนวคิดเรื่อง จำนวนเชิงวิธีจัดหมู่ (Combination Numbers) และจำนวนทวินาม (Binomial Numbers) และการศึกษาเรื่อง “จำนวนเชิงรูปภาพ” (Figurate numbers) ของนักคณิตศาสตร์ชาวกรีกด้วย
สามเหลี่ยมปาสคาล คือ อะไร?
สามเหลี่ยมปาสคาล มีต้นกำเนิดมาจากความช่างสังเกตของนักคณิตศาสตร์ ที่พบว่า เมื่อเรานำสัมประสิทธิ์
ที่ได้จากการกระจายทวินาม (a b)n มาเขียนเรียงกันเป็นรูปสามเหลี่ยมแล้ว ตัวเลขที่อยู่ข้างล่างของ
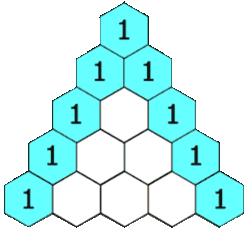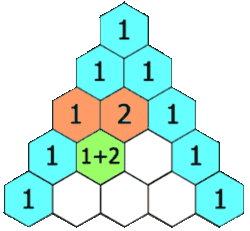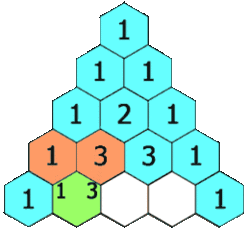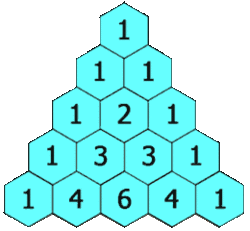
รูปสามเหลี่ยมจะมีค่าเท่ากับตัวเลขที่อยู่ข้างบน 2 ตัวที่อยู่เยื้องๆ กับตัวมันบวกกัน
พิจารณา (a b)n เมื่อ n เป็นจำนวนเต็มบวกต่างๆกัน
เมื่อ n = 0 => (a b)0 = 1เมื่อ n = 1 => (a b)1 = a b ส.ป.ส.เป็น 1 และ 1 ตามลำดับ
เมื่อ n = 2 => (a b)2 = a2 2ab b2 ส.ป.ส.เป็น 1, 2, 1 ตามลำดับ
เมื่อ n = 3 => (a b)3 = a3 3a2b 3ab2 b3 ส.ป.ส.เป็น 1, 3 , 3, 1 ตามลำดับ
เมื่อ n = 4 => (a b)4 = a4 4a3b 6a2b2 4ab3 b4 ส.ป.ส.เป็น 1, 4, 6 , 4, 1 ตามลำดับ
.
.
.
เอาเฉพาะสัมประสิทธิ์ดังกล่าวมาเขียนได้ดังนี้ n=0;1
n=1; 1 1
n=2; 1 2 1
n=3; 1 3 3 1
n=4; 1 4 6 4 1
จะเห็นว่าในบรรทัด n=2 ตัวเลข 2 เกิดจาก 1 1 ในบรรทัดn=1
และในทำนองเดียวกัน ในบรรทัด n=3 ตัวเลข 3 เกิดจาก 1 2 หรือ 2 1 ในบรรทัด n=2
ส่วนภาพด้านบนเป็นสามเหลี่ยมปาสคาล ของจำนวนเต็มบวก 10 ตัวแรกภายใต้รูปสามเหลี่ยมปาสคาลมีความมหัศจรรย์มากมาย
| 
